算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,比如排序就有十大经典排序和几种奇葩排序,虽然结果相同,但在过程中消耗的资源和时间却会有很大区别。
那么我们应该如何去衡量不同算法之间的优劣呢?
主要还是从算法所占用的「时间」和「空间」两个维度去考量。
- 时间维度:是指执行当前算法所消耗的时间,我们通常用「时间复杂度」来描述。
- 空间维度:是指执行当前算法需要占用多少内存空间,我们通常用「空间复杂度」来描述。
大O符号表示法
大O表示法:算法的时间复杂度通常用大O符号表述,定义为 **T[n] = O(f(n)) **。称函数T(n)以f(n)为界或者称T(n)受限于f(n)。
如果一个问题的规模是n,解这一问题的某一算法所需要的时间为T(n)。T(n)称为这一算法的“时间复杂度”。
大O符号是一种算法「复杂度」的「相对」「表示」方式。
这个句子里有一些重要而严谨的用词:
- 相对(relative):你只能比较相同的事物。你不能把一个做算数乘法的算法和排序整数列表的算法进行比较。但是,比较2个算法所做的算术操作(一个做乘法,一个做加法)将会告诉你一些有意义的东西;
- 表示(representation):大O(用它最简单的形式)把算法间的比较简化为了一个单一变量。这个变量的选择基于观察或假设。例如,排序算法之间的对比通常是基于比较操作(比较2个结点来决定这2个结点的相对顺序)。这里面就假设了比较操作的计算开销很大。但是,如果比较操作的计算开销不大,而交换操作的计算开销很大,又会怎么样呢?这就改变了先前的比较方式;
- 复杂度(complexity):如果排序10,000个元素花费了我1秒,那么排序1百万个元素会花多少时间?在这个例子里,复杂度就是相对其他东西的度量结果。
算法的空间复杂度通常也用大写的O符号来表示
常见的时间复杂度量级
我们先从常见的时间复杂度量级进行大O的理解:
- 常数阶O(1)
- 线性阶O(n)
- 平方阶O(n²)
- 对数阶O(logn)
- 线性对数阶O(nlogn)
- 立方阶O(n³)
- 指数阶(2^n)
- O(n!)
- K次方阶O(n^k)
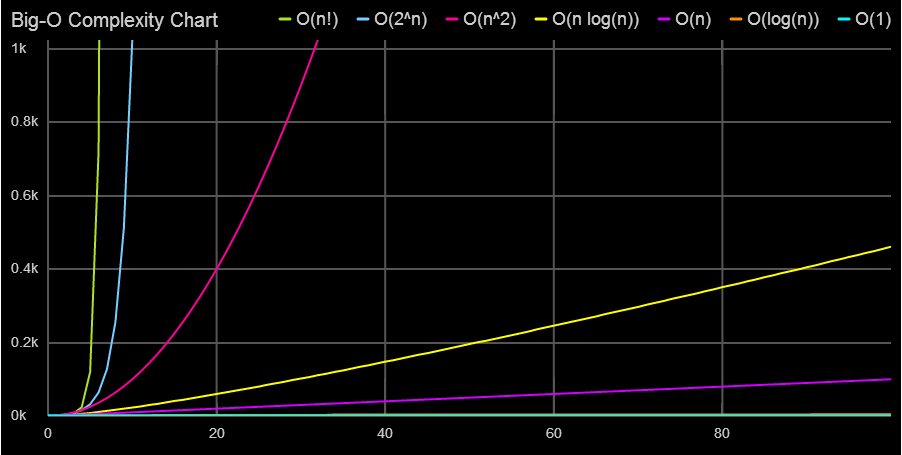
常见的时间复杂度高低排序:
O(1)<O(logn)<O(n)<O(nlogn)<O(n²)<O(n²logn)<O(n³)<O(2ⁿ)<O(n!)<O(nⁿ)
O(1)
O(1)就是最低的时空复杂度了,也就是耗时/耗空间与输入数据大小无关,无论输入数据增大多少倍,耗时/耗空间都不变。 哈希算法就是典型的O(1)时间复杂度,无论数据规模多大,都可以在一次计算后找到目标(不考虑冲突的话)
下面这段代码无论代码执行了多少行,其他区域不会影响到操作,这个代码的时间复杂度都是O(1)
def swap_two_ints(a, b)
a ,b = b, aO(n)
代表数据量增大几倍,耗时也增大几倍。比如常见的遍历算法
在下面这段代码,for循环里面的代码会执行 n 遍,因此它消耗的时间是随着 n 的变化而变化的,因此可以用O(n)来表示它的时间复杂度。
def sum(n):
ret = 0
for i in range(n):
ret += i
return retO(n²)
代表数据量增大n倍时,耗时增大n的平方倍,这是比线性更高的时间复杂度。比如冒泡排序,就是典型的O(n^2)的算法,对n个数排序,需要扫描n×n次
def bubblesort(nums):
for i in range(len(nums)-1):
for j in range(len(nums)-i):
if nums[j-1] > nums[j]:
nums[j-1], nums[j] = nums[j], nums[j-1]
return numsO(logn)
当数据增大n倍时,耗时增大logn倍(这里的log是以2为底的, 底数不管是2或者10再或者是其他数,可以把底数看成一个常数不会影响结果,通常把底数忽略不写,比如,当数据增大256倍时,耗时只增大8倍,是比线性还要低的时间复杂度)。二分查找就是O(logn)的算法,每找一次排除一半的可能,256个数据中查找只要找8次就可以找到目标
在二分查找法的代码中,通过while循环,成 2 倍数的缩减搜索范围,也就是说需要经过 log2^n 次即可跳出循环
def binary_search(nums, target):
l, r = 0, len(nums)-1
while l <= r:
mid = l + r //2
if nums[mid] == target:
return mid
if target > nums[mid]:
l = mid+1
else:
r = mid-1
return -1O(nlogn)
将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logn),也就是了O(nlogn)
def test(n):
i = 1
for i in n:
while i < n:
i *= 2参考上面的O(n²) 去理解就好了,O(n³)相当于三层n循环,其它的类似
空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度,同样反映的是一个趋势,我们用 S(n) 来定义。
空间复杂度比较常用的有:O(1)、O(n)、O(n²),定义一个变量就是O(1),定义一个数组就是O(n),定义一个二维数组就是O( n² )
常见算法时间对比图
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
| 冒泡 | O(n 2 ) | O(n 2 ) | 稳定 | O(1) | n 小时较好 |
| 交换 | O(n 2 ) | O(n 2 ) | 不稳定 | O(1) | n 小时较好 |
| 选择 | O(n 2 ) | O(n 2 ) | 不稳定 | O(1) | n 小时较好 |
| 插入 | O(n 2 ) | O(n 2 ) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(log R B) | O(log R B) | 稳定 | O(n) | B 是真数 (0-9) ,R 是基数 ( 个十百 ) |
| Shell | O(nlogn) | O(n s ) 1<s<2 | 不稳定 | O(1) | s 是所选分组 |
| 快速 | O(nlogn) | O(n 2 ) | 不稳定 | O(nlogn) | n 大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n 大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n 大时较好 |
数据规模的概念

以上数据可能根据各自机器性能,可能会有所不同,保守计算的话在各自规模上除以10应该是没有问题的。










Comments | NOTHING